Liczba π jest najbardziej znaną liczbą w matematyce.
Wyprzedza inne sławne liczby, których nazwy pochodzą od znanych matematyków, takie jak: liczba Eulera, liczba Grahama, liczba Fibonacciego, liczba Stirlinga, liczba Catalana, liczba Poissona, liczba Mersenne`a, liczba Ramseya. Nazwa liczby π nie pochodzi jednak od greckiego matematyka Pitagorasa, lecz od włoskich słów: perimetron – obwód lub periferia – obrzeże. Często spotyka się określenia dla liczby π jako stała Archimedesa lub ludolfina – od nazwiska XVI-wiecznego holenderskiego matematyka Ludolpha van Ceulena.
Liczba π stanowi stosunek obwodu koła do jego średnicy.
Jeśli na obwodzie koła zaznaczymy punkt (fioletowy znaczek) i przetoczymy koło poczynając od tego punktu i kończąc na nim, to dokonamy jednego pełnego obrotu koła. Gdy zmierzymy drogę przebytą w trakcie tego obrotu (bordowy odcinek), to okaże się, że odwód naszego koła jest równy nieco ponad trzem jego średnicom.

Fenomen liczby π ≈ 3,14 polega na tym, że jest to wartość stała, niezmienna, niezależna od rozmiarów koła. Czy koło jest ogromne, czy małe, π jest zawsze takie samo.
Oto ważne wzory, w których występuje liczba π:

O dziwo, liczba π jest na tyle uniwersalna, że pojawia się także w zagadnieniach zupełnie z kołem niezwiązanych, np. w analizie matematycznej, w teorii liczb, a również w rachunku prawdopodobieństwa, a także w teorii grawitacji Einsteina. Liczba π występuje w wielu matematycznych równaniach i wzorach, takich jak wzory Eulera czy wzór Stirlinga.
Wzmianki o liczbie Pi możemy znaleźć już w Biblii, w II Księdze Królewskiej. Czytamy w niej: „Stworzył morze z roztopionego metalu, o długości dziesięciu łokci od brzegu do brzegu; było idealnie okrągłe, o wysokości pięciu łokci i nić o długości trzydziestu łokci opasywała je naokoło”. Z podanych w tekście danych liczbowych wynika, że obwód okrągłego naczynia jest trzy razy dłuższy od jego średnicy. Także starożytni Babilończycy ok. 2000 lat p.n.e. zauważyli, że obwód okręgu jest ponad trzy razy dłuższy niż jego średnica. Również w piramidzie Cheopsa stosunek sumy dwóch boków podstawy do wysokości piramidy wynosi 3,1416. Jest to przybliżenie liczby π z dokładnością do czterech miejsc po przecinku! Czy to zadziwiający przypadek, czy wynik geniuszu ówczesnych budowniczych?
Ok. 225 roku p.n.e. Archimedes oszacował, że liczba π mieści się w przedziale między 223/71 a 220/70. Zasługę wprowadzenia oznaczenia tej liczby jako π przypisujemy Williamowi Jonesowi, który w XVIII w. piastował stanowisko naukowe w Towarzystwie Królewskim w Londynie. Do rozpowszechnienia tego oznaczenia w kontekście stosunków długości w kole przyczynił się głównie szwajcarski matematyk Leonhard Euler.
Dokładnej wartości liczby π nie poznamy nigdy, gdyż jest ona liczbą niewymierną. Jej rozwinięcie dziesiętne jest nieskończone i nie widać w nim żadnej powtarzalności ani wzorca dla następstwa cyfr. Ponadto π jest liczbą przestępną tzn. taką, która nie jest pierwiastkiem żadnego wielomianu o współczynnikach wymiernych. W 1882 roku Ferdinand Lindemann, w dość skomplikowany sposób, udowodnił przestępność liczby π.
Oto liczba π z pierwszymi dwudziestoma miejscami po przecinku: 3,14159265358979323846.
A oto rozwinięcie liczby π do ponad 50 tysięcy cyfr po przecinku: Liczba Pi (pdf).
Do wyznaczenia wartości liczby π można użyć szeregów liczbowych. Funkcjonują następujące wzory na przybliżenie liczby π:

Obliczanie dokładnej wartości liczby π postępowało coraz szybciej. W 1853 roku William Shanks ogłosił jej poprawną wartość aż do 527 miejsca po przecinku. We współczesnych czasach poszukiwanie coraz dokładniejszego rozwinięcia liczby π nabrało ogromnego przyspieszenia dzięki zaawansowanej technice komputerowej. W 1949 roku obliczono π z dokładnością do 2037. miejsca po przecinku, co zajęło 70 godzin pracy ogromnego komputera. Do 2002 roku obliczono π do porażającego 1 241 100 000 000 miejsca po przecinku, ale ogon liczby π wciąż przyrasta. Gdybyśmy stanęli na równiku i zaczęli zapisywać rozwinięcie liczby, wynik Shanksa zająłby „aż” 14 metrów, natomiast długość rozwinięcia z 2002 roku pozwoliłaby opasać kulę ziemską 62 razy!!! 🙂
Współcześnie stosuje się różne metody obliczania π, takie jak: metoda Monte Carlo, rozwinięcie w szereg Taylora oraz algorytmy bazujące na nieskończonych szeregach.
Metoda przybliżenia (aproksymacji) liczby π metodą Monte-Carlo, czyli punktów losowych.
Weźmy kwadrat o boku 2r i wpiszmy w niego okrąg o promieniu r, co przedstawia poniższy rysunek.
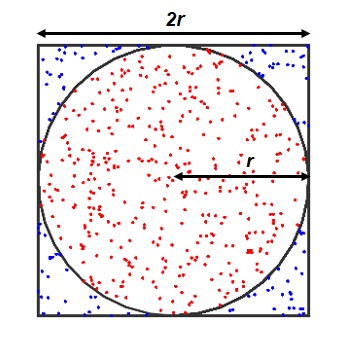
Pole kwadratu wynosi zatem Pk = 2r · 2r = 4r² zaś pole okręgu Po = πr²
Stosunek Po do Pk (po skróceniu r²) = π/4
Mnożąc obie strony równania przez 4 otrzymujemy 4⋅(Po/Pk) = π
Wybierając losowo punkty w kwadracie, jesteśmy pewni, że zastosowanie będzie miał wzór, który wyprowadziliśmy:
π = 4 · (liczba punktów w okręgu / liczba punktów w kwadracie)
Stosując komputer do losowego wyboru punktów wewnątrz kwadratu, obliczamy następnie jaki jest stosunek ilości punków czerwonych do wszystkich punktów (czerwonych plus niebieskich). Wynik tego dzielenia mnożymy przez 4 i otrzymujemy w przybliżeniu liczbę π. Oczywiście im więcej losowych punktów wybierzemy tym wynik obliczenia będzie bardziej zbliżony do rozwinięcia dziesiętnego liczby π. Przy 200 tyś. punktów, co dla komputera nie jest żadnym wygórowanym zadaniem, liczba π wynosi w przybliżeniu 3,141585, czyli jest dokładna do czterech miejsc po przecinku.
Na przestrzeni lat postawiono wiele pytań na temat liczby π:
- czy cyfry liczby π są rozmieszczone zupełnie losowo?
- czy można znaleźć w jej rozwinięciu każdy dowolnie zadany ciąg cyfr?
- czy w rozwinięciu występuje fragment 0123456789?
W latach pięćdziesiątych XX wieku odpowiedź na powyższe pytania wydawała się pozostawać poza możliwościami człowieka. Jednak w 1997 roku odnaleziono te kolejne cyfry występujące po sobie w liczbie π. Szukany ciąg cyfr zaczyna się na 17 387 594 880 miejscu po przecinku lub, posługując się przenośnią z długością równika, około 5000 km przed końcem pierwszej rundy dookoła świata. 🙂

Tak się składa, że rozkład częstotliwości występowania cyfr w pierwszym milionie miejsc po przecinku liczby π jest prawie jednakowy. Poszczególne cyfry pojawiają się w rozwinięciu liczby π prawie dokładnie tyle samo razy:
cyfra „0” – występuje 99 959 razy, cyfra „1” – występuje 99 758 razy,
cyfra „2” – występuje 100 026 razy, cyfra „3” – występuje 100 229 razy,
cyfra „4” – występuje 100 230 razy, cyfra „5” – występuje 100 359 razy,
cyfra „6” – występuje 99 548 razy, cyfra „7” – występuje 99 800 razy,
cyfra „8” – występuje 99 985 razy, cyfra „9” – występuje 100 106 razy.
Liczba π ma swoje pozytywne znaczenie w numerologii.
Suma jej 144 cyfr po przecinku daje wynik 666. Obie te liczby (144 i 666) mają bardzo pozytywny wydźwięk w numerologii. 144 oznacza korzystne zmiany i nowe pomysły, poparte siłą woli i determinacją w osiągnięciu celu. Zaś 666 jest niezwykle pozytywnym znakiem we wszechświecie, nakłaniającym do porzucenia negatywnych myśli i skupianiu się tylko na pozytywnym nastawieniu do życia.
Aby pomóc w zapamiętaniu fragmentu rozwinięcia liczby π, polski matematyk Witold Rybczyński w 1949 roku ogłosił konkurs na napisanie tzw. pi-poematu. Chodziło o to, aby liczba liter w poszczególnych słowach utworu poetyckiego odpowiadała kolejnym cyfrom liczby π. Sam pomysłodawca stworzył taką oto inwokację:
„Daj, o pani, o boska Mnemozyno, pi liczbę, którą też zowią ponętnie Ludolfiną, pamięci przekazać tak, by jej dowolnie oraz szybko do pomocy użyć; gdy się problemu nie da inaczej rozwiązać, pauza – to zastąpić liczbami.” (myślnik po „pauza” zastępuje zero)
Inny ciekawy wierszyk, w którym liczba liter wyrazów pokrywa się z kolejnymi cyframi liczby π, brzmi następująco: „Tak i mnie i tobie poznawana tu liczba cudna dla ogółu przynosi wszystkim pożytek wspaniały.” π ≈ 3,14159265358979
Corocznie 14 marca (3.14), głównie w USA z uwagi na sposób zapisu daty, obchodzone jest święto liczby π. Po raz pierwszy obchodzono to święto w 1988 roku, w San Francisco, w tamtejszym Exploratorium stanowiącym centrum światowej nauki. Z kolei w Europie 22 lipca obchodzony jest dzień aproksymacji liczby π, jako sposób zapisu daty w postaci ilorazu 22/7, co jest w przybliżeniu równe 3,1428.
Rekordzistą wpisanym do Księgi Guinnessa, który zapamiętał najwięcej cyfr liczby π jest Japończyk Akira Haraguchi. Podczas bicia rekordu, stosując specjalne techniki zapamiętywania, podał liczbę π z dokładnością do 100 tysięcy cyfr po przecinku.
Liczba π jest nie tylko przedmiotem matematycznych spekulacji, ale również symbolem ludzkiej zdolności do odkrywania i zgłębiania tajemnic otaczającego nas świata. Jej nieprzewidywalność i niekończąca się liczba dziesiętna przypominają nam, że niektóre rzeczy mogą pozostawać poza naszym pełnym zrozumieniem, ale właśnie to skłania nas do wciąż trwających badań i eksploracji. Wnioski płynące z liczby π sięgają daleko poza matematykę, ukazując nam piękno i nieuchronną tajemniczość wszechświata. Dlatego właśnie, liczba π pozostaje nie tylko częścią wiedzy matematycznej, ale także symbolem głębszych aspektów naszego poznania i dążeń do zgłębiania rzeczywistości.
Serdecznie zapraszam do zapoznania się z moją ofertą korepetycji z matematyki na poziomie szkoły podstawowej bądź średniej – korepetycje z matematyki Łódź-Bałuty.
Bądź jak π – rozwijaj się bez końca, bo edukacja nie ma granic!



