Definicja liczby pierwszej
Liczba pierwsza to liczba naturalna większa od 1, która ma tylko dwa dzielniki: „1″ i samą siebie. Mówiąc najprościej, liczba pierwsza to liczba, która jest podzielna bez reszty tylko przez siebie. Dziesięć początkowych liczb pierwszych to: 2, 3, 5, 7, 11, 13, 17, 19, 23 i 29.
Historia liczb pierwszych rozpoczyna się 300 lat p.n.e. kiedy to Euklides objaśnił, że ilość liczb pierwszych jest nieograniczona. Następnie 200 lat p.n.e. Eratostenes z Cyreny stworzył narzędzie do oddzielania liczb pierwszych od pozostałych liczb złożonych – tzw. sito Eratostenesa.
Weźmy zbiór liczb, spośród których będziemy szukać liczb pierwszych. Niech to będą liczby od 1 do 30.
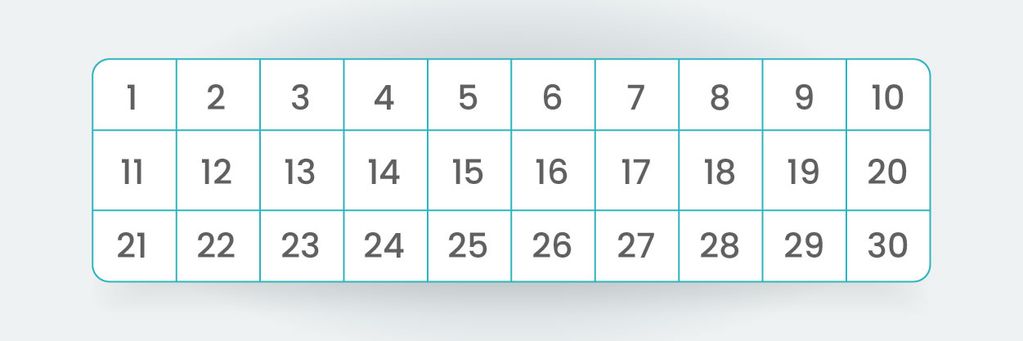
Liczbę „1” pomijamy, gdyż zgodnie z definicją liczba pierwsza jest większa od jedności. Przechodzimy do kolejnej liczby „2”, która okazuje się być liczbą pierwszą, gdyż dzieli się tylko przez 1 i przez samą siebie. Następnie szukamy wielokrotności tej napotkanej liczy pierwszej, czyli wielokrotności „2”. Na zielono oznaczamy liczbę pierwszą, a na czerwono jej wielokrotności, które z pewnością nie są liczbami pierwszymi.
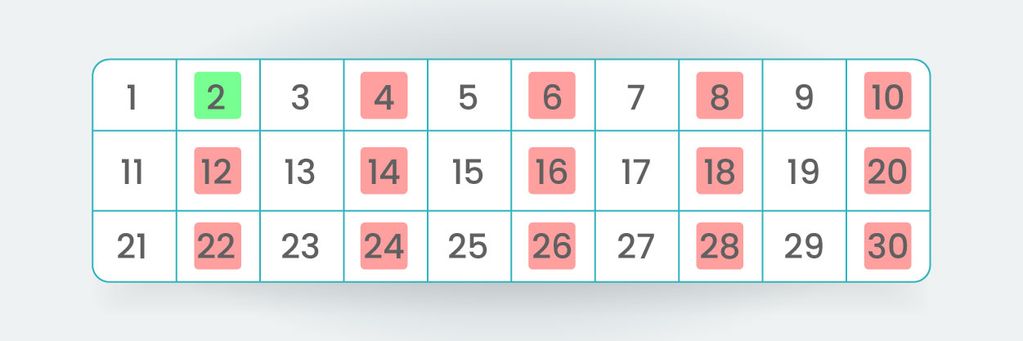
Przechodzimy teraz do kolejnej liczby niezmalowanej na czerwono, czyli do liczby „3”, która jest liczbą pierwszą, gdyż dzieli się bez reszty tylko przez samą siebie. Następnie szukamy wielokrotności tej liczby „3”, które na pewno nie są liczbami pierwszymi. Otrzymujemy następujący zbiór liczb:
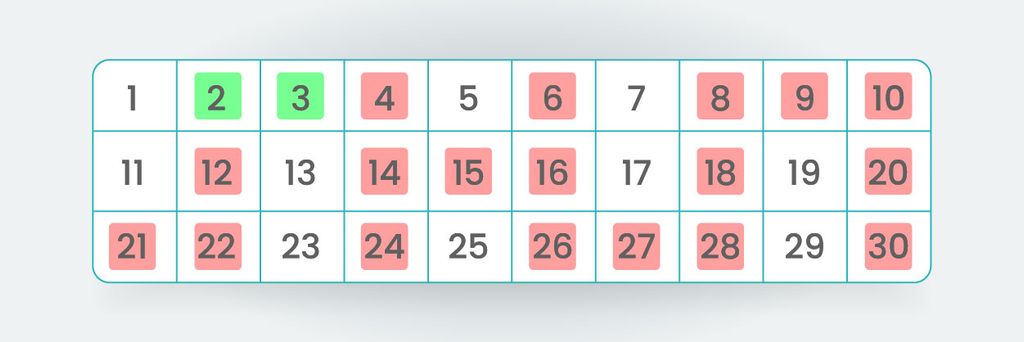
Kolejną liczbą niezaznaczoną jeszcze na czerwono jest liczba „5”, która jest z pewnością liczbą pierwszą. Znowu znajdujemy jej wielokrotności i zaznaczmy je na czerwono. W ten sam sposób postępujemy z kolejnymi napotkanymi liczbami pierwszymi – zaznaczamy na czerwono ich wielokrotności, o ile nie były już wcześniej zaznaczone. Ostateczny wynik poszukiwania liczb pierwszych wygląda następująco:
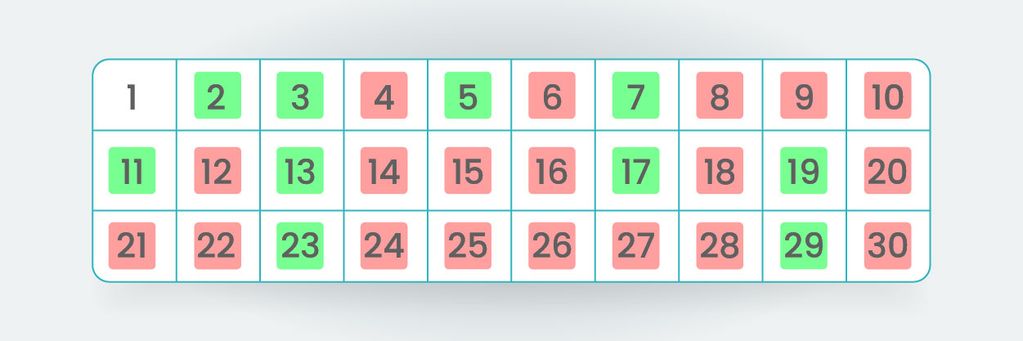
Tak więc liczy pierwsze w zakresie od 0 do 30 są następujące: 2, 3, 5, 7, 11, 13, 17, 19, 23 i 29.
Można próbować wyznaczać tą metodą liczby pierwsze w szerszym zakresie liczbowym, jednak jest to powolne i dość pracochłonne, choć rezultat wykluczania wielokrotności liczb pierwszych daje zawsze prawidłowy wynik w postaci zbioru kolejnych liczb pierwszych.
Zapraszam do zapoznania się z moją ofertą korepetycji z matematyki – Łódź Bałuty.



